Altera Integer Arithmetic IP - Manual (Page 139)

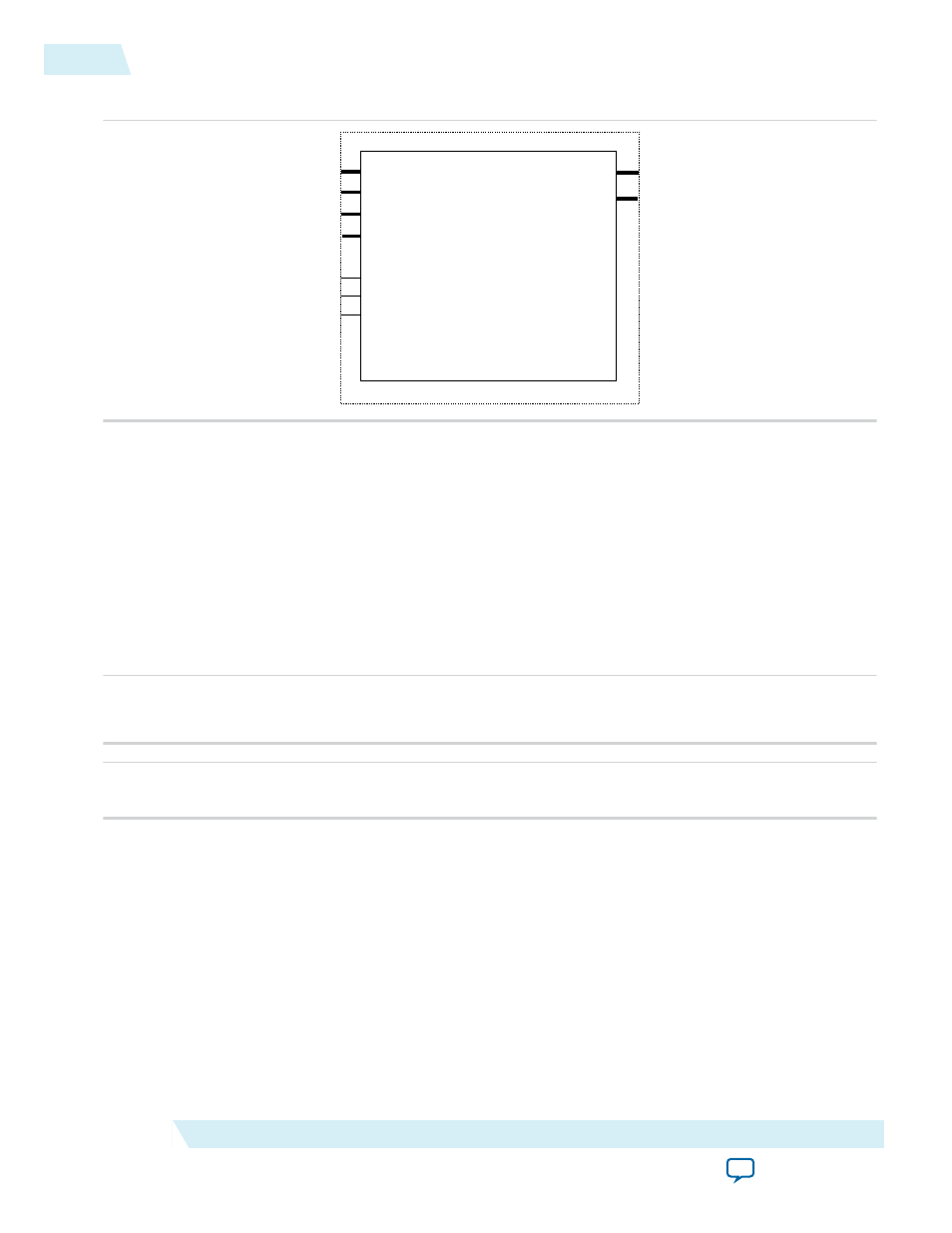
Figure 10-1: ALTMULT_COMPLEX Ports
dataa_real
inst
ALTMULT_COMPLEX
datab_real
dataa_imag
result_real
datab_imag
clock
ena
aclr
result_imag
Complex Multiplication
Complex numbers are numbers in the form of the following equation:
a + ib
Where:
• a and b are real numbers
• i is an imaginary unit that equals the square root of -1:√-1
Two complex numbers, x = a + ib and y = c + id are multiplied, as shown in the following equations.
xy = (a + ib)(c + id)
= ac + ibc + iad – bd
= (ac – bd) + i(ad + bc)
Related Information
Canonical Representation on page 10-2
Canonical Representation
From Complex Multiplication equation, the multiplication of two complex numbers can be represented in
two parts: real and imaginary.
The following equation shows that the xy_real variable represents real representation.
10-2 Complex Multiplication
UG-01063
2014.12.19
Altera Corporation ALTMULT_COMPLEX (Complex Multiplier)
Send Feedback