Casio ClassPad II fx-CP400 User Manual
Page 120
Chapter 5: Differential Equation Graph Application
120
Graphing a Second Order Differential Equation
This section explains how to input a second order differential equation, draw a phase plane, and graph the
solution curve(s). With this application, a second order differential equation is input in the form of a set of two
first order differential equations.
• A phase plane is the family of solutions of either a second order differential equation or two first order
differential equations of the form
x
’ =
dx
/
dt
=
f
(
x
,
y
) and
y
’ =
dy
/
dt
=
g
(
x
,
y
). A single second order differential
equation can also be graphed, but it must be written as two first order differential equations.
• You can overlay, onto the phase plane, solution curves of the second order differential equation input on the
[DiffEq] tab for given initial conditions.
u To input a second order differential equation and draw a phase plane
0503
To input {
x
’ =
x
,
y
’ = −
y
} and draw its phase plane
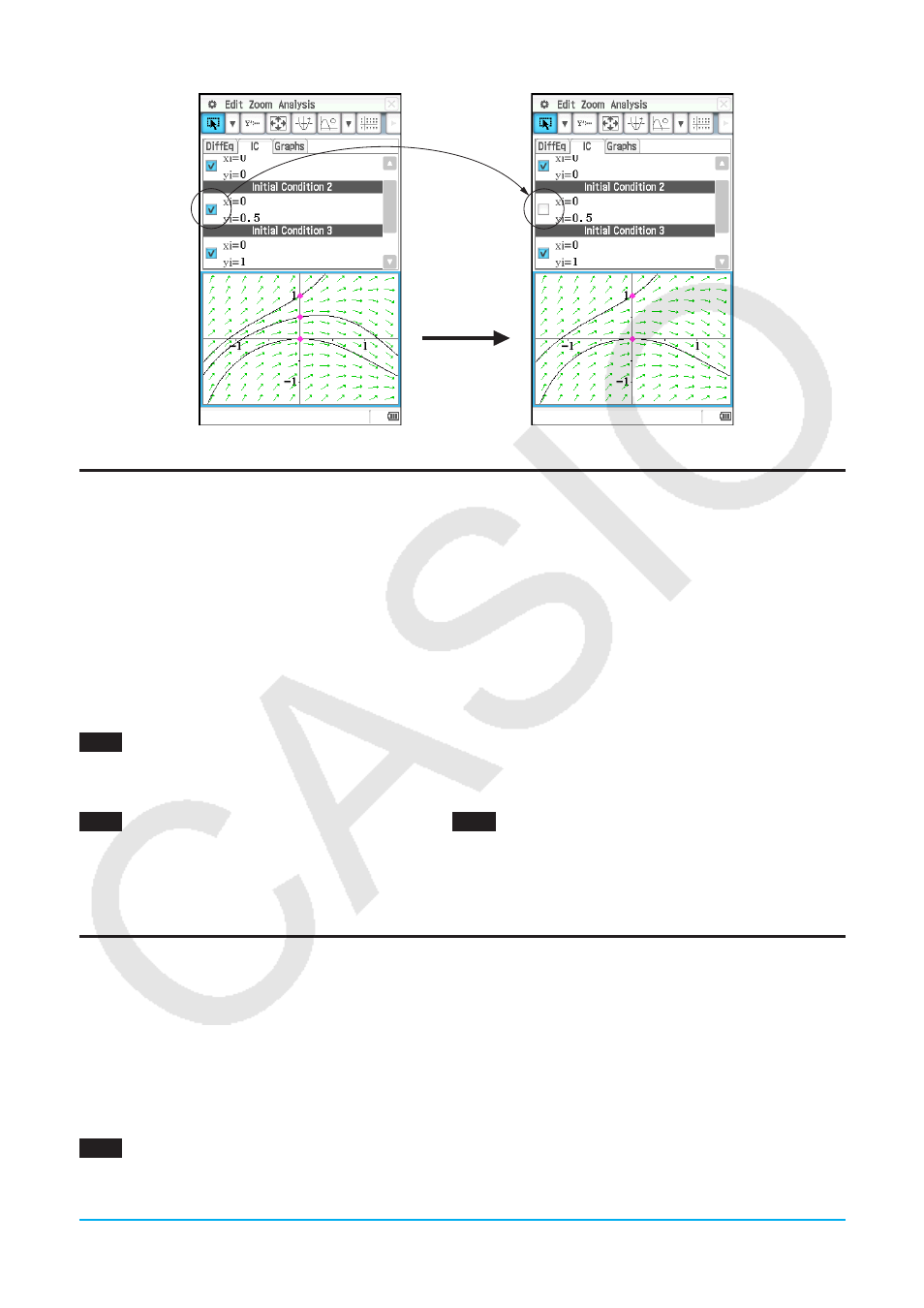
u To input initial conditions and graph the solution curves
0504
After performing the operation under example
0503
, to graph the solution curve of the initial condition
(
xi
,
yi
) = (1, 1)
Independent variable minimum value (
t
min) = −7.7, maximum value (
t
max) = 7.7, and initial value
(
t
0) = 0
Graphing an Nth-order Differential Equation
This section explains how to graph the solution curve(s) for an
n
th-order (higher order) differential equation
based on specified initial conditions. With this application, an
n
th-order differential equation is input in the form
of a set of multiple first order differential equations.
Note:
For
n
th-order differential equations, only solution curves are drawn.
u To input an
n
th-order differential equation and initial conditions, and then graph the solution
curves
0505
To specify the three initial conditions (
xi
,
y
1
i
,
y
2
i
) = (0, −1, 0), (0, 0, 0), (0, 1, 0) for the differential
equation
y
” =
x
−
y
, and graph its solution curves